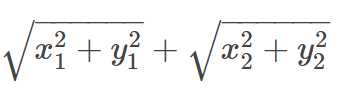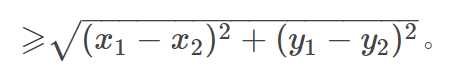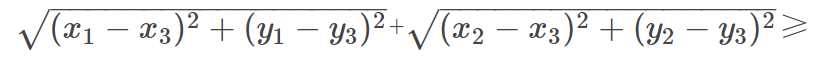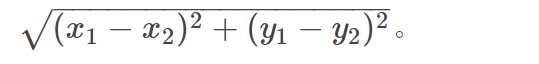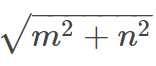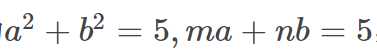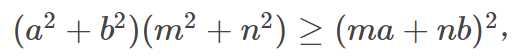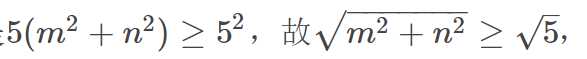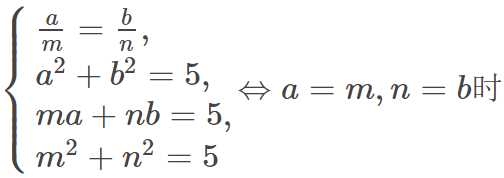柯西不等式定理及其变式：高考数学高频考点梳理

柯西不等式，包括了二维形式、向量形式、三角形式、积分形式以及一般形式等，本文为大家整理了柯西不等式定理和形式，同时还包括柯西不等式的应用技巧等，具体为若a,b,c,d都是实数，则：当且仅当时，ad=bc时等号成立。

一、二维形式的柯西不等式

定理1：（二维形式的柯西不等式）

若a,b,c,d都是实数，则：，当且仅当时，ad=bc时等号成立。

定理2：（柯西不等式的向量形式）

设α,β两个向量，则|α⋅β|≤|α||β|，当且仅当β是零向量，或存在实数k，使α=kβ时，等号成立。

定理3：（二维形式的三角不等式）

设x1,y1,x2,y2∈R，那么

在定理3中，用x1−x3代x1，用y1−y3代y1，用x2−x3代x2，用y2−y3代y2可得平面三角不等式：

二、一般形式的柯西不等式

定理：（一般形式的柯西不等式）

设a1,a2,a3,⋯,an,b1,b2,b3,⋯,bn是实数，则

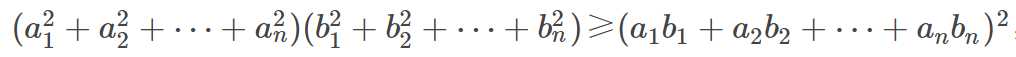，当且仅当bi=0(i=1,2,⋯,n)或存在一个数k，使得ai=kbi(i=1,2,⋯,n)时，等号成立。

柯西不等式的主要应用是证明不等式和求最值，利用柯西不等式证明不等式时，先使用拆项、重组、填项等方法技巧构造符合柯西不等式的应用条件，再处理；利用柯西不等式求最值时，一定要注意验证等号成立的条件。

构造符合柯西不等式的形式及条件，可以巧拆常数，可以重新安排各项的次序，可以填项，也可以改变式子的结构。

三、柯西不等式例题

设a,b,m,n∈R,且a2+b2=5,ma+nb=5，则

的最小值为___

A. 根号5、B. 根号6、C. 根号3、D. 根号2

答案：A

解析：因为

，所以由柯西不等式得

于是

当且仅当

，等号成立，所以

的最小值为根号5。

为了方便大家阅读公式图片，本文提供图片版阅读：