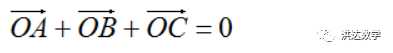三角形重心性质证明：高中几何重点结论与例题精讲

三角形的有关内容中，“四心”的性质是一个绕不开的话题，它在平面几何及立体几何中都有诸多的关联及应用。本文探讨下重心的有关性质，并给出证明过程。

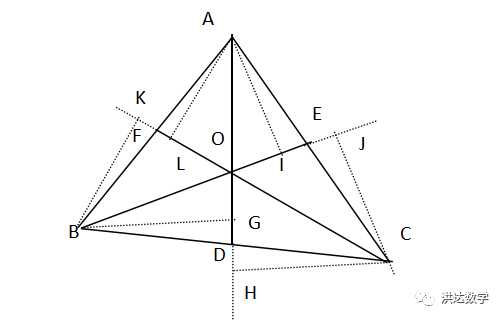
重心就是三角形的三条边上的中线的交点，如图所示，三角形ABC中，BC边上的中点D,AC边上的中点E交于O点，连接CO并交AB边于F点，求证：F为AB的中点（即O为重心）。

证明：延长AD，BE,并作BG⊥AD,CH⊥AD延长线于D点，作BE⊥AI,CJ⊥BE延长线于J点，

由全等三角形的性质可以得到，△BGD全等于△CHD,△AEI全等于△CEJ,

因此得到BG=CH,AI=CJ,

所以得到S△AOB=S△AOC,S△AOB=S△AOC=S△BOC,

延长CF并作AL⊥CF,BK⊥CF延长线于K点，

通过上面证明，可以得到△BKF全等于△ALF,

因此得到BF=AF，题目要求得证。

通过上述证明过程，我们还能得到

三角形重心的性质1：重心与三角形顶点组成的三个三角形面积相等。

与此同时，再介绍重心的另外性质：

三角形重心的性质2：重心到顶点的距离与到对边中点的距离比为2：1。

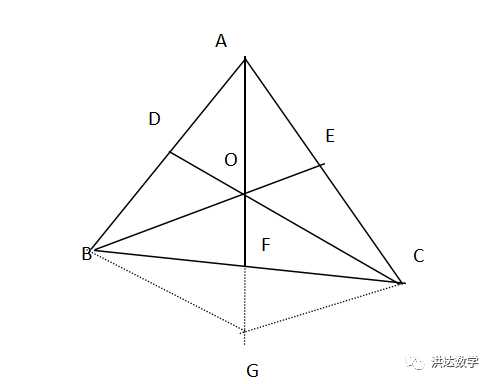
证明：如图作CG//AF延长线于G点，连接BG。

由相似三角形性质可以得到AE/EC=AO/OG,

所以AO=OG,

又BF=FC,∠BFA=∠CFG,∠BOG=∠OGC,

所以得到三角形BOF全等于三角形CGF，

所以OF=FG,

所以AO:OF=2:1,

证明完毕。

由性质2，容易得到三角形重心的性质3：重心到顶点的向量的和为0.即：

由性质3，容易得到三角形重心的性质4：在平面直角坐标系中，重心的坐标是顶点坐标的算数平均数。

三角形重心的性质5：三角形的重心是三角形内到三角形距离之积最大的点。

证明性质5：

设O为三角形内一点，则OD,OE,OF分别是BC，AC,AB上的垂线，则

三角形重心性质6：重心为到三角形顶点距离平方和最小的点。